$$(xy)(x^2y^2)=4xy3\tag{1}$$ Let $X=xy, Y=xy$ then we get $$X^32XY4Y3 = 0\tag{2}$$ Hence $Y=1/2(X^33)/(X2)$ We can get ${x,y}$ by solving for $t^2XtY=0$ Since discriminant must be positive, we know that $2\leqq X\leqq2$ Thus equation $(2)$ has intger solutions $(X,Y)=(1,2)$ Solving for $t^2t2=0$, we get $t=1$ and $2$The given equation $ {{x}^{2}}4xy{{y}^{2}}6x2yk0 $ (i) represent the point of straight line, if $ \Delta =0, $ where $ \Delta =abc2fgha{{f}^{2}}b{{g}^{2}}c{{h}^{2}}=0 $ (ii)4xyy2=x(xy)y' 4xyy to the power of 2=x(xy)y' Similar expressions
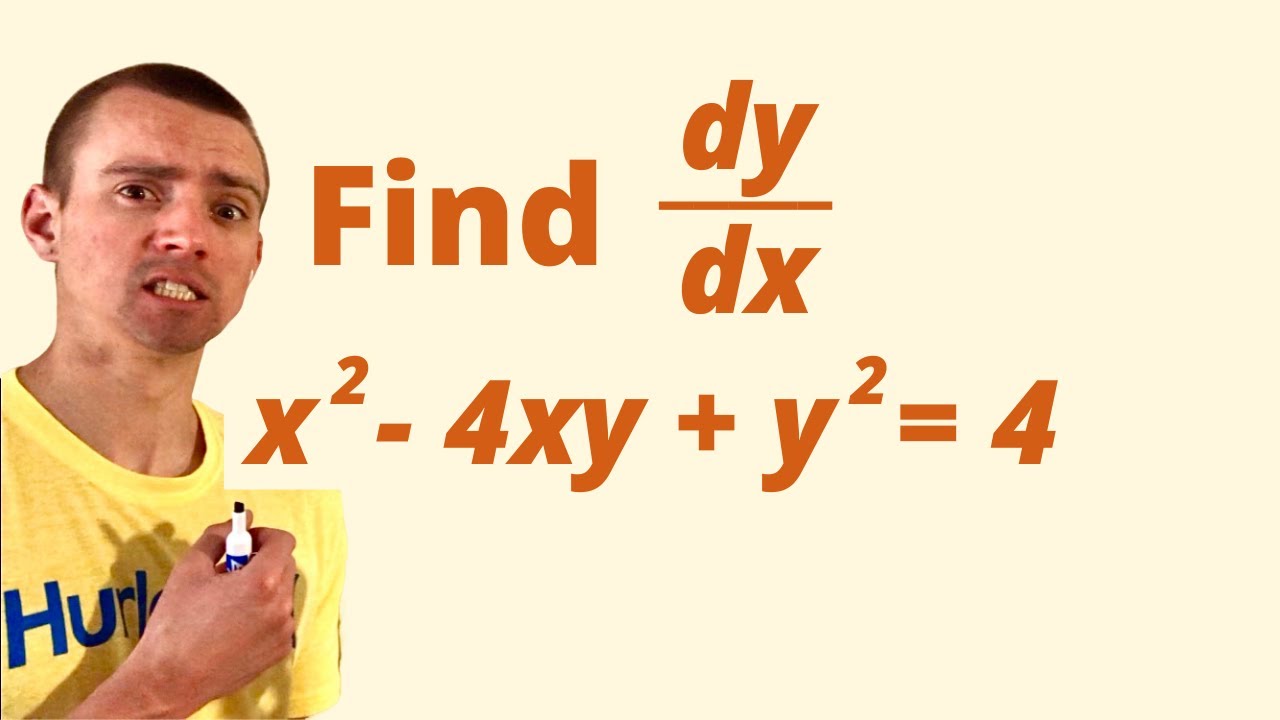
Find Dy Dx By Implicit Differentiation X 2 4xy Y 2 4 Youtube
